Caso 1
Podemos sumar y restar radicales solamente cuando estos tengan el mismo índice y contengan una misma base (subradical o radicando).
Ejemplo:
Se pide realizar una operación combinada de suma y resta, lo cual podremos hacer ya que todos los términos tienen
Para recordar:
Cuando hay un radical solo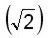 siempre será lo mismo que 
.
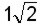Cuando hay un radical solo
siempre será lo mismo que .
Como los radicales son todos iguales 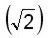se suman los números que están fuera de ellos (3 + 5 + 1) y la parte radical se deja igual.
se suman los números que están fuera de ellos (3 + 5 + 1) y la parte radical se deja igual.
Veamos ahora otro ejemplo:
Como todos los términos tienen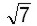 
podemos sumar y/o restar sin problema. Se ha añadido un "1" delante del radical único 
.
podemos sumar y/o restar sin problema. Se ha añadido un "1" delante del radical único .
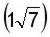Caso 2
¿Podremos sumar y restar radicales que tengan el mismo índice pero que tengan distinta base?
Ejemplo:
Aquí también se pide realizar una operación combinada de suma y resta. Sin embargo, no será posible porque los tres radicales poseen el mismo índice (2) y sus bases (o cantidades subradicales o radicandos) son diferentes, además de que son números primos y no se pueden factorizar.
Pero, veamos otro ejemplo:
Esta también es una operación combinada de sumas y restas de radicales que tienen el mismo índice (2) pero tienen distinta base. Pero aquí hay una diferencia: las bases se pueden factorizar, de tal modo que
| 108 |
2
|
54
|
2
|
27
|
3
|
9
|
3
|
3
|
3
|
1
| |
27
|
3
|
9
|
3
|
3
|
3
|
1
|
| 75 |
3
|
25
|
5
|
5
|
5
|
1
|
Para quedar
0 comentarios:
Publicar un comentario