CONJUNTOS NUMÉRICOS NATURALES

Los primeros números que el hombre inventó fueron los números naturales, los cuales se utilizaban y se utilizan para contar elementos de un conjunto finito, ya que se procede a enumerar dichos números de una manera ordenada, seleccionándolos uno tras otro a la vez que se le atribuye a cada uno un número. Los números naturales sirven para contar y ordenar fundamentalmente.

El nombre “Números Naturales” seguramente proviene debido a que estos números son los que aparecen por primera vez en el proceso natural de contar o enumerar los objetos de un conjunto. Los símbolos 1, 2, 3, .... etc., se llaman numerales hindú-arábigos.

Los Números naturales empiezan en el UNO y pueden llegar a cualquier cifra, pues siempre es posible agregar uno más. El CERO no se incluye en los naturales.

Los hindúes hicieron grandes y valiosos aportes en matemáticas a la humanidad. Los sacerdotes hindúes inventaron los números que usamos, llamados arábigos por ser los árabes quienes los divulgaron. Los contactos comerciales entre la India y el imperio construido por los árabes favorecieron que éstos últimos adoptaran tanto el sistema de numeración hindú como sus signos numerales, contribuyendo luego decisivamente a difundirlos en Occidente.

 Además, los hindúes inventaron el valor de la cifra cero (en el siglo IX el cero ya era de uso común en los textos hindúes), muchas nociones sobre decimales, nuestro sistema de valorar un número según el lugar que ocupa en el conjunto de varias cifras y los fundamentos del álgebra y la trigonometría. Al inventarse el CERO, éste más los naturales formaron el Conjunto de los Números Cardinales.

                             

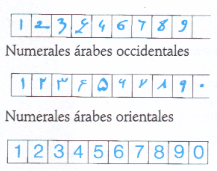
Este esquema muestra la evolución de las cifras indoarábigas en su paso de oriente a occidente a lo largo de la Edad Media. Los numerales actuales derivan de esas cifras.

Historia del cero

Hasta el año 1200 después de Cristo, se usó en Europa la numeración romana.  Por esa época, un mercader de Pisa, Leonardo Pisano, más conocido como Fibonacci, al volver de un largo viaje por África y Oriente Medio escribió un libro titulado Liber Absci, donde exponía y proponía emplear el sistema de numeración utilizado por los árabes, que a su vez lo habían aprendido de los hindúes.  Sus ventajas más importantes eran la utilización del cero y el sistema posicional de notación.

La obra de Leonardo Pisano tuvo que esperar a la invención de la imprenta para que llegara a ser conocida en toda Europa.

   Es interesante señalar que ya los mayas, en el siglo V, tenían la noción del cero, número que empleaban en su sistema de numeración vigesimal.  El número cero es una de las grandes invenciones del genio humano, ya que facilita la ejecución de las operaciones aritméticas.

Su introducción en Europa permitió el progresivo abandono de la numeración romana vigente hasta la Edad Media. Puede comprobarse la importancia del cero, si se si      hacen los cálculos corrientes utilizando los números romanos.  Se verá que el más sencillo cálculo aritmético se ha convertido en algebraico.

N = { 1, 2, 3, 4, 5, 6, 7,.......}

El conjunto de los Números Naturales surgió de la necesidad de contar, lo cual se manifiesta en el ser humano desde sus inicios.

Este conjunto se caracteriza porque:

Tiene un número ilimitado de elementos

Cada elemento tiene un sucesor y todos, excepto el 1, un antecesor.

El sucesor de un número natural se obtiene sumando uno (+1); el antecesor se obtiene restando uno (-1).

2) N* = N₀ = Conjunto de los Números Cardinales

N ₀ =  { 0, 1, 2, 3, 4, 5, 6,.....}

Al Conjunto de los Números Naturales se le agregó el 0 (cero) y se forma el Conjunto de los Números Cardinales. 

3) Z  =  Conjunto de los Números Enteros

NUMEROS ENTEROS Z

Desde hacía mucho tiempo, los chinos utilizaban bastoncillos de bambú o de madera para representar los números y realizar, en especial, cálculos comerciales de una manera práctica, pero también para tratar cuestiones relacionadas con los aumentos y disminuciones de magnitudes, o con distancias recorridas en sentidos opuestos; esos bastoncillos eran negros o rojos según que representaran cantidades positivas o negativas, de acuerdo con una atribución del color que es justamente la opuesta a la empleada en la contabilidad occidental.

Los matemáticos hindúes del siglo VI  mencionan también el uso de números negativos para tratar este tipo de problema. Los antiguos griegos, por el contrario, rechazaron que pudieran existir tales números.

En Europa medieval, los árabes dieron a conocer los números negativos de los hindúes,  que en el siglo XII se utilizaban ya ocasionalmente para designar las pérdidas en el análisis de cuestiones financieras.  Durante el Renacimiento, el manejo práctico de esos números en la contabilidad y otros contextos ayudó a su lenta introducción en las matemáticas.

El alemán Michael Stifel  (1487-1567), monje agustino convertido al protestantismo y amigo personal de Lutero, fue uno de los primeros en admitir el uso de coeficientes negativos para el estudio de las ecuaciones cuadráticas y divulgó el uso del signo menos “―“ para designar la resta; de hecho, los signos + y ― estaban ya en uso  entre los comerciantes alemanes del siglo XV para indicar el exceso o el defecto de mercancías en los almacenes. Con todo, la consideración de las cantidades negativas como correspondientes a números matemáticamente legítimos alcanzó aceptación general hasta el siglo XVIII, cuando los números negativos empezaron a ser entendidos como opuestos de los positivos.

En la matemática moderna el conjunto de los números enteros (Z) abarca todos los enteros tanto negativos como positivos, y llega hasta el infinito hacia ambos lados de una recta numérica, por tanto, en rigor no existe un comienzo, salvo que como tal se considere el CERO (el cual agregado al conjunto de los números naturales forma el conjunto de los Cardinales).

Operaciones en Z (con enteros positivos y negativos)

Para poder realizar las operaciones en el conjunto de los números enteros (Z) debes memorizar las siguientes reglas (son fáciles; sólo requieren de práctica).

Suma en Z (Conjunto de Números Enteros positivos y negativos):

Existen únicamente dos casos: números de igual signo y números con signo distinto. Las reglas a memorizar son las siguientes:

a) Números de igual signo: Cuando dos números tiene igual signo se debe sumar y conservar el signo.

Ejermplos :        – 3   +  – 8  =   – 11      ( sumo y conservo el signo)

                         12   +   25  =   37       ( sumo y conservo el signo)

b) Números con distinto signo: Cuando dos números tienen distinto signo se debe restar y conservar el signo del número que tiene mayor valor absoluto (recuerda que el valor absoluto son unidades de distancia, lo cual significa que se debe considerar el número sin su signo).

Ejemplo:          – 7   +   12   =   5    (tener 12 es lo mismo que tener  +12, por lo tanto, los números son de distinto signo y se deben restar: 12  –  7  =   5 ¿con cuál signo queda? El valor absoluto de –7 es 7 y el valor absoluto de  +12 es 12, por lo tanto, el número que tiene mayor valor absoluto es el 12; debido a esto el resultado es un número positivo).

                    5   +   – 51   =   – 46   ( es negativo porque el 51 tiene mayor valor absoluto)

                   – 14  +   34   =    20

Resta en Z

Para restar dos números o más, es necesario realizar dos cambios de signo (uno después del otro) porque de esta manera la resta se transforma en suma y se aplican las reglas mencionadas anteriormente. Son dos los cambios de signo que deben hacerse:

a)         Cambiar el signo de la resta en suma y

b)         Cambiar el signo del número que está a la derecha del signo de operación por su signo contrario

Ejemplo 1:

     –3  –  10   

a) cambiamos el signo de resta por el de suma:

  –3    +  10 

b) cambiamos el signo del número que está a la derecha del signo de operación (que ahora es el +):

– 3 + – 10 =    –13   ( signos iguales se suma y conserva el signo)

Ejemplo 2:

19  –   – 16 

a) cambiamos el signo de resta por el de suma:

19 + –16

b) cambiamos el signo del número que está a la derecha (– 16) del signo de operación (que ahora es el +):

19 + + 16 =   19   +    16    =    35

Ver: PSU: Matemática; Pregunta 03_2006

Multiplicación y División en Z

La regla que se utiliza es la misma para multiplicar que para dividir. ¿CÓMO SE HACE? Multiplico los números y luego multiplico los signos de acuerdo a la siguiente tabla:

+   •    +    =    +

–   •   –     =    +

+   •   –     =   –

–  •   +     =   –

Ejemplos:   – 5   •    – 10   =    50    (  5  •   10   =    50 ;   –  •   –   =   + )

                     12  •    – 4    =   – 48    (  12 •   4   =     48;:    + •  –   =   – )

Siempre se deben multiplicar o dividir los números y luego aplicar las reglas de signos para dichas operaciones (las reglas de signos para la suma son para la suma y no deben ser confundidos con los de estas otras operaciones).

Z =   { ..... –3, -2, -1, 0, 1, 2, 3,...}

El Conjunto de los Números Enteros surge de la necesidad de dar solución general a la sustracción, pues cuando el sustraendo es mayor que el minuendo, esta sustracción no tiene solución en los Conjuntos Naturales y Cardinales (por ejemplo: 5 – 20 =  ¿?). Debido a esto, la recta numérica se extiende hacia la izquierda, de modo que a cada punto que representa un número natural le corresponda un punto simétrico, situado a la izquierda del cero. Punto simétrico es aquel que está ubicado a igual distancia del cero (uno a la derecha y el otro a la izquierda de él).

Z = N*  U Conjunto de los Números Enteros negativos

Z = Tiene 3 Subconjuntos:

Enteros Negativos: Z ^¯

Enteros Positivos:  Z ⁺

Enteros Positivos y el Cero:  Z ₀⁺

Por lo tanto, el Conjunto de los Números Enteros es la unión de los tres subconjuntos mencionados.                     

    Z  =  Z ¯  U  {0}  U  Z ⁺

 

4) Q = Conjunto de los Números Racionales

Q  = {....- ¾, - ½, - ¼ , 0, ¼ , ½, ¾,.....}

El conjunto de los Números Racionales se creó debido a las limitaciones de cálculo que se presentaban en el conjunto de los Números Naturales, Números Cardinales y Números Enteros. Por ejemplo, sólo se puede dividir en el conjunto de los Números Enteros si y sólo si el dividendo es múltiplo, distinto de cero, del divisor. Para solucionar esta dificultad, se creó este conjunto, el cual está formado por todos los números de la forma a / b. Esta fracción en la cual el numerador es a, es un número entero y el denominador b, es un número entero distinto de cero. (Ver: Fracciones)

El conjunto de los Números Racionales (Q ) se ha construido a partir del conjunto de los Números Enteros (Z). 

Se expresa por comprensión como:

Q  =  {  a / b  tal que  a y b 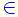   Z; y  b  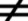  0 }

Este conjunto se representa gráficamente, dividiendo cada intervalo de una recta numérica en espacios iguales, que representen números enteros. Cada una de estas subdivisiones representa una fracción con denominador igual al número de partes de la subdivisión. 

Cada fracción es un número racional y cada número racional consta de infinitas fracciones equivalentes.

5) I =  Q* = Conjunto de Números Irracionales

NUMEROS IRRACIONALES

Cuando dividimos entre sí dos números naturales, por lo general llegamos a un número exacto, aunque sea después de colocar muchos decimales; pero la operación se cierra, obteniendo como resultado otro número natural. En forma recíproca, ese resultado podemos expresarlo de nuevo como fracción.

Sin embargo, existen algunos números que no permiten ser expresados como fracción. Son números cuya cantidad de decimales es infinita, nunca se acaban sus decimales, así es que no se pueden expresar como cociente de dos números naturales. Estos son los llamados números irracionales.

Un número irracional es un número no racional; es decir, que no se puede expresar en forma fraccionaria.

No deben confundirse con los números racionales, porque éstos son números decimales finitos, infinitos periódicos e infinitos semiperiódicos que sí pueden transformarse en una fracción, por ejemplo: 18/5 que es igual a 3,6 por lo tanto es un número racional a diferencia de la raíz cuadrada de 2 en cuyo resultado se obtienen infinitos decimales, y su fraccionamiento resulta imposible.

Hipaso de Metaponto.

Historia de los irracionales

Según se sabe, fue en el siglo VII antes de Cristo cuando los griegos descubrieron los números llamados irracionales. La acción se le atribuye a un discípulo de Pitágoras, Hipaso, quien usando elementos geométricos intentó calcular la raíz cuadrada de 2 para escribirla como fracción, lo cual le resultó imposible.

Como las fracciones son raciones (porciones, partes) del todo, y ese número no podía ser racionado, pasó a ser un número irracional. Inicialmente los llamaron números inconmensurables.

En esa época el método geométrico imperaba, aunque sí trabajaban con raíces cuadradas y cúbicas, pero, sin embargo, no conocían los números negativos y  el cero, ni tampoco tenían un sistema de símbolos literales bien desarrollado.

Fue en China, hacia los siglos II y I a. C, donde por primera vez usaron coeficientes negativos y se dieron reglas para operar con ellos.

Pero fueron los indios, entre los siglos V y XV,  quienes inventaron el sistema de numeración actual, introdujeron los números negativos y comenzaron a operar con los números irracionales de forma semejante que con los racionales, sin representarlos geométricamente.

Al final de cualquier número irracional se suelen colocar puntos suspensivos (...) para indicar que nunca se puede llegar al último decimal, siempre hay otro detrás.

El Conjunto de los Números Irracionales se simboliza por I o bien por Q*. A él pertenecen todos los  números decimales infinitos puros, es decir aquellos números que no pueden transformarse en una fracción.

Un número irracional es todo número decimal infinito no periódico.

El conjunto de los números Irracionales se define por comprensión como: Q* = { x / x tiene un desarrollo infinito no periódico}

I  =   Conjunto de Números Decimales Infinitos no Periódicos

Este conjunto surgió de la necesidad de reunir a ciertos números que no pertenecen a los conjuntos anteriores; entre ellos se pueden citar a las raíces inexactas, el número Pi, etc. A él pertenecen todos los números decimales infinitos puros, es decir aquellos números que no pueden transformarse en una fracción. No deben confundirse con los números racionales, porque éstos son números decimales finitos, infinitos periódicos e infinitos semiperiódicos que sí pueden transformarse en una fracción.

Ejemplos:  1,4142135....

                               0,10200300004000005....      

Números reales

Se representan con la letra .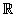 

El conjunto de los Números Reales (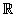) está integrado por:

• El conjunto de los Números Racionales () que corresponden a la unión de todos los números cuya expresión decimal es finita, infinita periódica o infinita semiperiódica.

• El conjunto de los números enteros, positivos y negativos, más el cero

• El conjunto  de los Números Irracionales (I)  que está formado por la unión de todos los números que admiten una expresión infinita no periódica.

Entonces, se llaman Números Reales a todos aquellos que se pueden expresar en forma decimal finita o infinita; es decir, el conjunto de los Números Reales (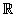) está formado por los elementos del conjunto  unido con I .

El siguiente cuadro es ilustrativo: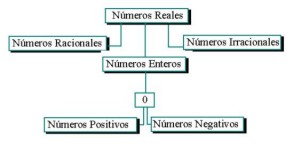

Todos los números reales pueden ser  representados en la recta numérica.

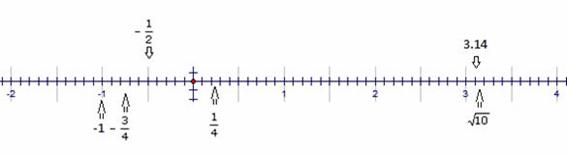
A cada punto de la recta numérica le corresponde un número real y viceversa; es decir, existe una correspondencia uno a uno entre los puntos de la recta numérica y los números reales.

Importante:

Con números reales pueden realizarse todo tipo de operaciones básicas con dos excepciones importantes:

1.- No existen raíces de orden par (cuadradas, cuartas, sextas, etc.) de números negativos en números reales, razón por la cual existe el conjunto de los números complejos donde estas operaciones sí están definidas.

2.- No existe la división entre cero, pues carece de sentido dividir entre nada o entre nadie; es decir, no existe la operación de dividir entre nada.

En otras palabras, no son reales las fracciones con denominador cero y las raíces de índice par y radicando negativo.

Infinito no es un número real

Infinito no es un número real, es una idea. Una idea de algo que no termina.

Recuerde, además, que cualquier fracción con  numerador cero, tiene como resultado final, el cero (cero dividido cualquier cosa es igual a cero)