POLINOMIOS

En matemáticas, un polinomio (del latín polynomius, y este del griego, πολυς [polys] ‘muchos’ y νόμος [nómos] ‘regla’, ‘prescripción’, ‘distribución’)1 2 3 es una expresión matemática constituida por un conjunto finito de variables (no determinadas o desconocidas) yconstantes (números fijos llamados coeficientes), utilizando únicamente las operaciones aritméticas de suma, resta y multiplicación, así como también exponentes enteros positivos. En términos más precisos, es una relación n-aria de monomios, o una sucesión de sumas y restas de potencias enteras de una o de varias variables indeterminadas.

Es frecuente el término polinómico (ocasionalmente también el anglicismo polinomial), como adjetivo, para designar cantidades que se pueden expresar como polinomios de algún parámetro, como por ejemplo: tiempo polinómico, etc.

Los polinomios son objetos muy utilizados en matemáticas y en ciencia. En la práctica, son utilizados en cálculo y análisis matemáticopara aproximar cualquier función derivable; las ecuaciones polinómicas y las funciones polinómicas tienen aplicaciones en una gran variedad de problemas, desde la matemática elemental y el álgebra hasta áreas como la física, química, economía y las ciencias sociales.

SIMPLIFICACION

Para otros usos de este término, véase Simplificación (desambiguación).

En lógica proposicional, la simplificación¹ ² ³ (equivalente a la eliminación de la conjunción) es una inferencia inmediata válida, forma de argumento y regla de inferenciaque hace que la inferencia de que, si la conjunción A y B es cierta, entonces A es verdad y B también es verdad. La regla permite acortar las pruebas más largas mediante la derivación de una de las conjunciones de una conjunción en una línea por sí misma.

Un ejemplo en español:

Llueve y llueve a cántaros.

Por lo tanto, está lloviendo.

La regla se puede expresar el lenguaje formal como:

\frac{P \land Q}{\therefore P}

o como

\text{[math]}

donde la regla es que cada vez que aparecen las instancias de "

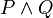P \and Q

" en las líneas de se puede colocar en una prueba, "

P

" o "

Q

" en una línea posterior.

SUMA Y RESTA DE RADICALES

Caso 1

Podemos sumar y restar radicales solamente cuando estos tengan el mismo índice y contengan una misma base (subradical o radicando).

Ejemplo:

Se pide realizar una operación combinada de suma y resta, lo cual podremos hacer ya que todos los términos tienen

Para recordar:
Cuando hay un radical solo

siempre será lo mismo que

Como los radicales son todos iguales

se suman los números que están fuera de ellos (3 + 5 + 1) y la parte radical se deja igual.

Veamos ahora otro ejemplo:

Como todos los términos tienen

podemos sumar y/o restar sin problema. Se ha añadido un "1" delante del radical único

Ver: Raíz: Operaciones combinadas

Caso 2

¿Podremos sumar y restar radicales que tengan el mismo índice pero que tengan distinta base?

Ejemplo:

Aquí también se pide realizar una operación combinada de suma y resta. Sin embargo, no será posible porque los tres radicales poseen el mismo índice (2) y sus bases (o cantidades subradicales o radicandos) son diferentes, además de que son números primos y no se pueden factorizar.

Pero, veamos otro ejemplo:

Esta también es una operación combinada de sumas y restas de radicales que tienen el mismo índice (2) pero tienen distinta base. Pero aquí hay una diferencia: las bases se pueden factorizar, de tal modo que

108	2
54	2
27	3
9	3
3	3
1

27	3
9	3
3	3
1

75	3
25	5
5	5
1

Para quedar

RACIONALIZACIÓN DE RADICALES

Cuando tenemos fracciones con radicales en el denominador conviene obtener fracciones equivalentes pero que no tengan radicales en el denominador. A este proceso es a lo que se llama racionalización de radicales de los denominadores.

Según el tipo de radical o la forma de la expresión que aparece en el denominador, el proceso es diferente.

Se pueden dar varios casos:

Si el denominador contiene un solo término formado por una sola raíz cuadrada. En este caso basta multiplicar numerador y denominador por la misma raíz cuadrada.

Por ejemplo, si queremos racionalizar el denominador de la fracción , multiplicaremos numerador y denominador por

Otro ejemplo. Racionalizar

Si antes de racionalizar extraemos los factores que se puedan en el radical del denominador, tenemos:

Ahora basta multiplicar numerador y denominador por para eliminar la raíz del denominador:

También se puede directamente multiplicar numerador y denominador por

Y ahora extraemos factores de la raíz del numerador y simplificamos.

, como vemos da el mismo resultado.

Si el denominador de la fracción contiene dos términos en uno de los cuales o en los dos hay una raíz cuadrada, se multiplica numerador y denominador por el conjugado del denominador. O sea si es una suma se multiplica por la resta, y viceversa.

Por ejemplo, multiplicamos numerador y denominador por

En el denominador siempre va a aparecer un producto de una suma por una diferencia, o sea una expresión del tipo

Otro ejemplo: , ahora multiplicamos numerador y denominador por

Si el denominador sólo tiene un término con una raíz de índice cualquiera, n, se multiplica numerador y denominador por otra raíz de índice n quecomplete una potencia de exponente n.

Por ejemplo: